燕东数据派 2024年10月16日 17:00 北京

近日，陈松蹊教授团队的研究论文《Statistical Inference for Four-regime Segmented Regression Models》被《统计年刊》（The Annals of Statistics）接受发表。

分段回归模型（segmented regression models）作为一类介于全局参数模型和非参数模型之间的回归模型，兼具着模型可解释性和稳健性的优点。但因其目标函数的非规则性，分段回归模型的优化和统计推断面临着更多的挑战。本文考虑了一类较为灵活的分段回归模型，不仅在模型形式上对现有文献进行了推广，并且对于优化算法、渐进性质的刻画和推断方法都做出了突破和改进。

本文的主要理论和方法贡献有如下方面：

（1）克服了变点模型（change-point model）和结构变化模型（structual change model）等单变量平行分段模型的局限性。本文中模型的划分平面为多变量的线性组合所构成的超平面，使得模型形式更为灵活，划分方式更加数据驱动；

（2）提出了一种混合整数二次规划算法（MIQP）以解决优化目标函数的非凸性，实现高效计算；

（3）首次在时间相依数据以及固定门阀效应下给出了划分超平面系数估计的大样本性质，通过多维复合泊松过程对其渐进分布实现精细刻画，证明了多个平面系数估计之间存在渐进独立性；

（4）提出一种光滑回归自助法（smoothed regression Bootstrap）进行统计推断，克服传统Bootstrap方法对于分段回归模型失效的挑战；

（5）提供了一种基于向后筛选的模型选择方法选择最优分段个数，并证明了模型选择的相合性。

文章提出的模型在北京空气污染的实际数据集中得到良好的应用效果。通过分段回归建模，文章发现PM2.5和气象变量（如风速、温度和湿度）的关系在不同季节可由三到四段的分段模型刻画，分别对应着污染的形成、传输和清洗的不同阶段，表明文章提出的分段模型在有良好拟合效果的同时具有物理可解释性。

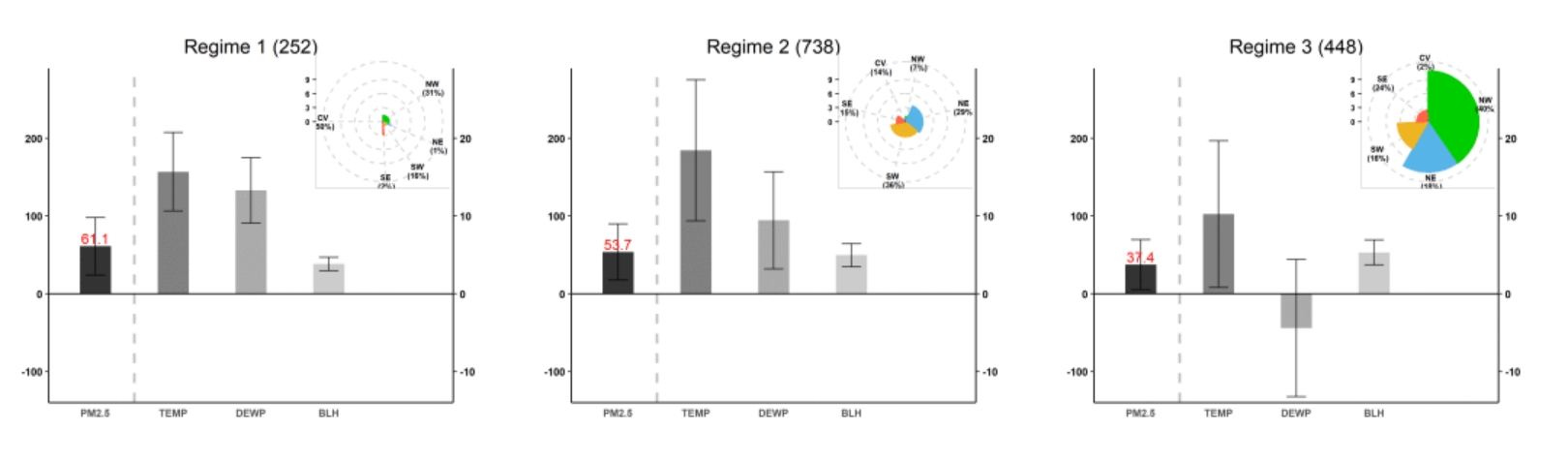
图1: 2019年北京秋季PM2.5和气象变量的分段回归模型中各划分区域内的关键变量。三个划分区域分别对应着污染开始、传输和清洗阶段。

本文的第一作者为北京大学光华管理学院2020级博士生闫晗，陈松蹊教授为通讯作者，也是闫晗的博士生导师。研究得到了国家自然科学基金项目Nos.12292980, 12292983和No.92358303的资助。

论文原文链接：

https://songxichen.com/Uploads/Files/Publication/Segmented_Regression_Model.pdf