Our new paper has just been published at https://proceedings.mlr.press/v202/tong23a.

Domain generalization (DG) is a fundamental problem in the field of machine learning, aiming to transfer knowledge from several source domains to a target domain without the use of target data during the training process. Due to the change in the distributions between source and target data, model may exhibit overfitting problem in the sense that the model trained on the source domains often performed poorly on the target domain.

This study proposed a distribution free domain generalization (DFDG) algorithm for classification. It seeks for low-dimensional invariant feature representations among different source domains and avoids minority domains or classes dominating the training process by utilizing a special standardization method. DFDG calculates the cross domain and cross class discrepancies by a kernel based paired two-sample test statistics. The selected invariant features are required to have both strong classification capability and small cross-domain variability. The introduced standardization method showed a better performance with fewer hyperparameters, allowing the use of more powerful computationally intensive classifiers in the whole procedure. The study also derived a generalization bound for kernel-based domain generalization methods in multi-class classification problems. Superior performance has been achieved in simulation and three real image classification tasks.

Domain Generalization and DFDG Algorithm

The domain generalization problem addresses datasets with the same classification classes from different sources. It assumes that the data distributions from different datasets are independently and identically drawn from a common super-population. The goal is to find cross-domain invariant features during the training process without using any target domain information, ensuring optimal classification performance over the entire super-population.

The DFDG method first maps data from the original feature domain to a high-dimensional reproducing kernel Hilbert space (RKHS), and then defines cross domain and cross class discrepancies using the Maximize Mean Discrepancy (MMD) statistic. The features sought by the algorithm reside in a low-dimensional subspace of the high-dimensional RKHS, which have minimum cross domain discrepancy and maximum cross class discrepancy simultaneously. The paper also introduced two normalization methods focusing on the first and second moments of paired MMD statistics, respectively. The extracted low-dimensional invariant features can be fed into k-nearest neighbor (KNN) or support vector machine (SVM) depend on the complexity of the classification problem.

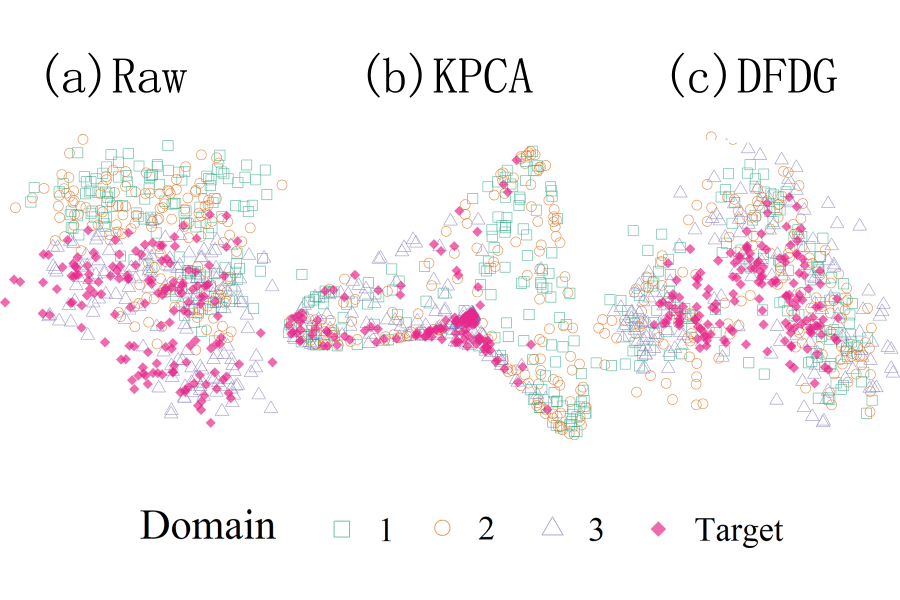
Figure 1: raw feature (a) and the extracted domain-invariant features (b: KPCA, c: DFDG)

Generalization Bound Theory

This study established a generalization bound for DFDG. Under some regularization conditions and given the confidence level, the excess risk converges to zero if both the sample size and the domain number over the class number go to infinity. Moreover, the study showed that larger number of classes and higher invariant feature dimensions will loose the generalization bound.

Experimental Results

We compare the proposed DFDG with the existing DG methods on a synthetic dataset and three real image classification tasks. The two proposed DFDG metrics DFDG-Eig and DFDG-Cov associated with two classifiers, the 1-nearest neighbor (1-NN) and the support vector machine (SVM), are used for comparison.

A two-dimensional dataset with 4 domains and 3 classes was drawn from different Gaussian distributions for the simulation study. As shown in Table 1, the proposed DFDG outperformed all the kernel DG methods even using only one hyperparameter with the 1-NN classifier. The performance was further lifted by using the SVM classifier with more hyperparameters for the kernel bandwidths and the SVM penalty.

We considered three datasets, the Office+Caltech, VLCS and Terra Incognita in case study. As shown in Table 2, DFDG outperformed existing algorithms in 11 out of 16 cases and achieved the second-best performance in 12 cases. Additionally, DFDG requires fewer hyperparameters, providing a computational advantage. On the imbalanced Terra Incognita dataset, Table 3 demonstrates that DFDG exhibited superior performance compared to the ERM baseline (neural network method) and existing kernel DG methods, highlighted the effectiveness of the proposed methods for imbalanced data.

Table 1. Mean and standard deviation of the classification accuracy of the synthetic experiments on 6 cases for different methods, where bold red and bold black indicate the best and second best respectively. And #hp denotes the number of hyperparameters.

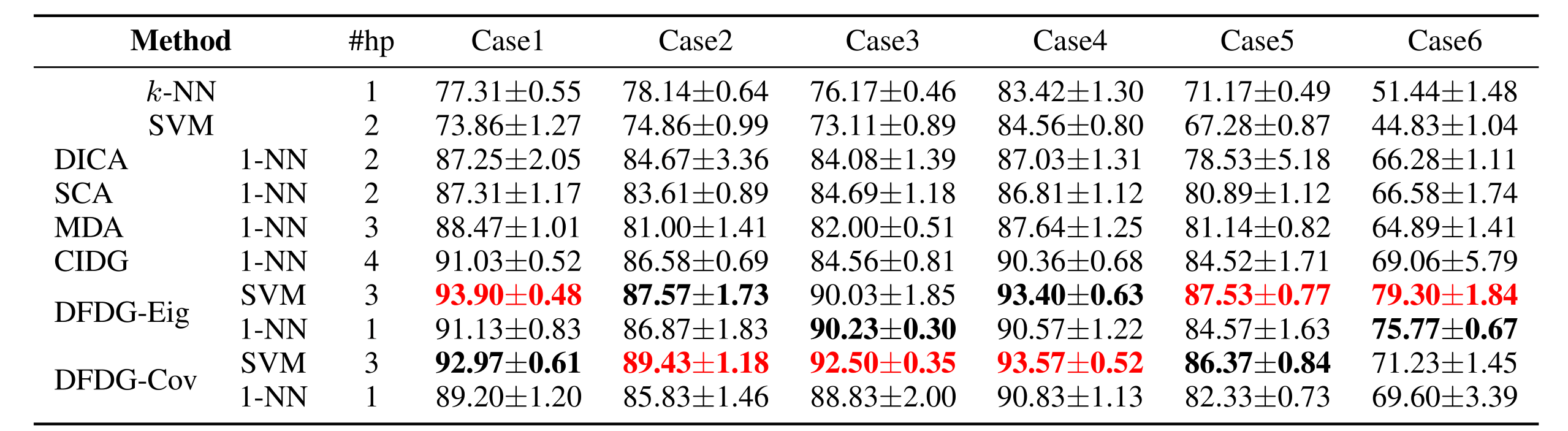
Table 2. Accuracy in Office+Caltech and VLCS datasets where bold red and bold black indicate the best and second best, respectively

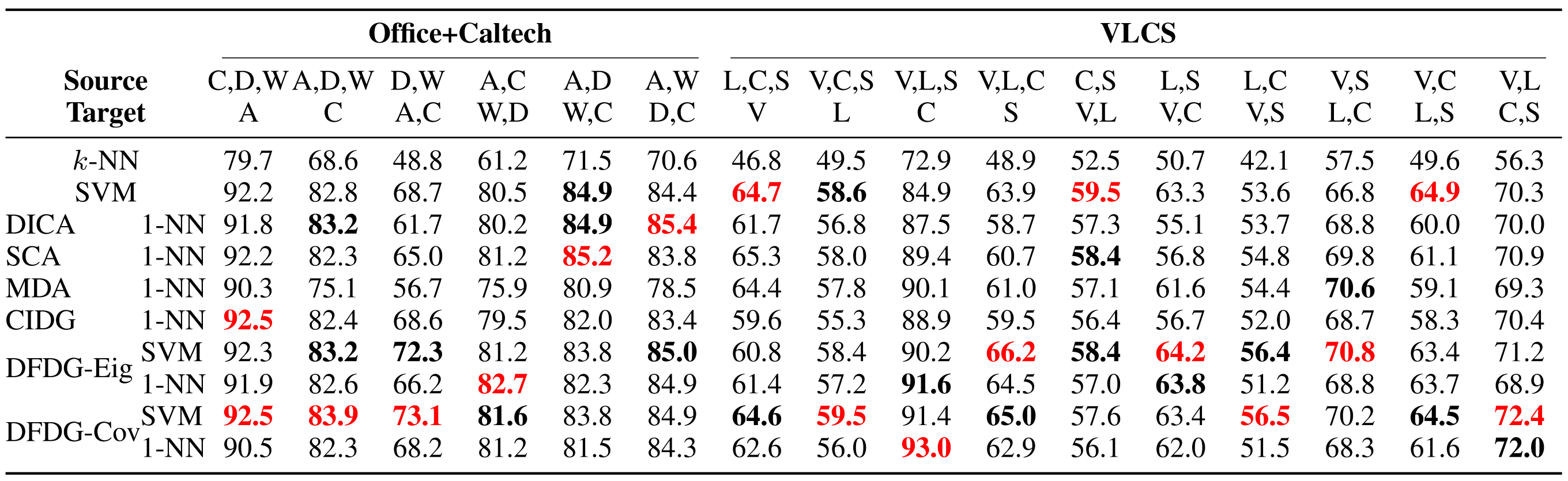
Table 3. Accuracy in the Terra Incognita dataset, where bold red and bold black indicate the best and second best, respectively

The first author of this paper is Tong Peifeng (Ph.D. student at Guanghua School of Management, Peking University), and the other authors include Su Wu (Ph.D. student at the Institute of Advanced Interdisciplinary Studies, Peking University), Li He, Ding Jialin, Zhan Haoxiang (undergraduate students at the School of Mathematical Sciences, Peking University), and Professor Chen Song Xi (corresponding author). The research was supported by the National Natural Science Foundation of China (Grant No. 12026607).